When you purchase through links on our site, we may earn an affiliate commission. Here's how it works. |
This advanced shutter time calculator for astrophotography operates beyond basic “500 Rule” calculations because it employs an intricate geometric system that determines the exact fastest shutter speed that works for your camera and lens setup to preserve star points as distinct points instead of developing into trails.
The main difficulty in untracked astrophotography occurs because the camera does not move with Earth's continuous rotation.
The duration of your exposure time determines how much the stars will seem to shift across your sensor, while the size of your camera pixels determines the total time at which this movement becomes visible to your eyes when looking at the image. The calculator solves this problem by determining the total elapsed time for a star to move beyond your specified tolerance threshold. This helps to calculate the optimum shutter speed for photographing astrophotography images with minimal star trails.
The Entry Fields
- Sensor Format: Choose the size of your camera's sensor. You can choose full-frame, Canon or Sony sized APS-C camera sensors, or Micro Four Thirds.
- Megapixels: The number of megapixels that your camera's sensor has.
- Focal Length: The focal length of your lens (not the effective focal length if you are using a crop camera; we calculate that out automatically)
- Trailing Tolerance: the maximum length in pixels of an acceptable star trail caused by the Earth's rotation.
- Target Declination: The declination direction of how your camera is pointing up from the horizon. Horizon is 0 degrees, and the pole is 90 degrees. The reason for this is that the apparent motion of the stars is more at the Celestial Equator than it is at the Celestial Poles. Normal declination is around 30 degrees for the Milky Way and should be good enough for most calculations.
CanonRumors Star Motion Shutter Speed Limit Calculator
Calculates max exposure based on resolution and movement.
1 pixel = Strict minimum movement. Use between 4 to 7, or your own acceptable length of star trails.
0° is the fastest-moving part of the sky. 30° for the Milky Way Core.
The Math
The core of the calculation is derived from a geometric-focused relationship that predicts star movement across the sensor plane, using a specific formula:
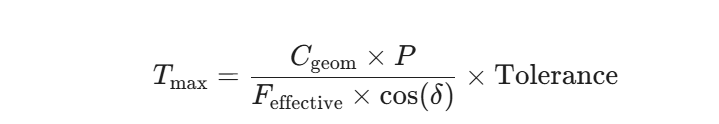
The formula demonstrates that the highest possible shutter speed (Tmax) depends on the relationship between the geometric limit, which depends on P, and the angular movement, which depends on Feffective and δ, before applying your selected tolerance factor. Eh, you asked.
Now, about the calculation definitions. Cgeom is a constant derived based on the Earth's rotational speed. It's a little more complicated than that, but that would explode this article and my brain again. It's set to a constant of 5.65 as a rough approximation. The first critical factor is the Pixel Pitch measurement, denoted as P. The physical size of a single pixel on your camera sensor measures in micrometers (μm). The calculator performs P calculation based on your sensor configuration and megapixel rating. Having the P value is important because the exposure time for cameras with small, dense pixels needs to be shorter because the star's apparent motion requires less time to cross the small pixel width.
Next, the calculator accounts for the magnification of star movement through the effective focal length (Feffective), which is the actual focal length of your lens multiplied by your sensor's crop factor. The longer the Feffective, the more magnified the star movement becomes on the sensor, and thus you must use a proportionally shorter exposure time to freeze the motion.
The calculator also includes a Star Motion Correction based on the sky's position, known as Declination (δ). The apparent speed of stars across the sky is fastest near the Celestial Equator (δ=0∘) and slowest near the Celestial Poles (δ=±90∘). By inputting the declination of the area you are photographing (e.g., ±30∘ for the Milky Way core), the calculator applies the cos(δ)1 correction factor, adjusting the shutter speed to account for the slower motion and providing the longest possible exposure time for that specific region of the sky.
The Trailing Tolerance allows you to add your individual preferences to the scientific process. The number of pixel movements for star objects that you will tolerate in your final image needs to be determined. The geometric formula determines the shortest possible path of a 1-pixel trail, which represents the smallest amount of movement that can be seen. The 1 pixel tolerance ensures perfect pinpoints, but it produces exposures that may be too brief for making high-quality, low-noise images.
Your exposure time will extend when you set the tolerance to more pixels because this setting allows you to collect more light, which results in a better signal-to-noise ratio and produces only a tiny acceptable trail that becomes invisible during regular viewing and printing. Your nightscape photograph will achieve its highest quality through the perfect combination of bright elements and defined details.
Photo by Usukhbayar Gankhuyag on Unsplash